Electrical Head Modeling |
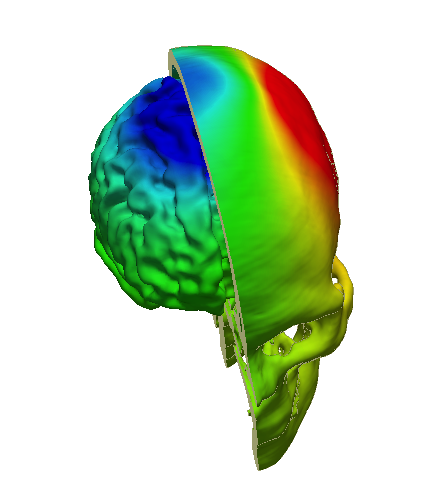 |
The observed EEG signal on the surface of the scalp arise from currents within the head due to dipolar sources in the cerebral cortex. The difficult problems of source localization and impedance imaging require modeling and simulating the associated bio-electric fields. Electrical Head Modeling research at the NeuroInformatics Center is focused on developing high-performance computational methods for analyzing head volume conduction with high resolution, individual head tissue geometries. The electrical forward problem consists of solving for the potentials induced for a given set of cortical current sources. This forward problem is well-posed and has a unique solution governed by Poisson's equation, the quasi-static approximation of Maxwell's equations. Solving the forward problem starts from a given set of current source configuration, the geometry of the head tissues and their conductivities. Then the potentials at the scalp electrodes can be calculated by solving the Poisson equation.
The forward electrical head modeling represents a core technology that enables much of the other research at the NeuroInformatics center. Source localization using the distributed dipole framework relies on repeatedly solving the forward problem for a large number of dipole sources covering the cortex. Inferring the conductivities of brain tissues through Electrical Impedance Tomography (EIT) relies on repeatedly solving the forward problem, while searching over conductivity values. For these reasons, together with the high resolution tissue geometries available from MR Imaging, computational efficiency and leveraging of High Performance computational resources for the solvers is important. At the NeuroInformatics Center we have developed two forward solvers based on Finite Difference Method. The first one considers only isotropic tissue conductivities and based on the ADI algorithm. The second one allows including anisotropy and is based on vector additive implicit method. Both solvers are parallelized on shared memory using OpenMP and on GPU using CUDA.